EXPRESIÓN DE LORENTZ

  -EXPRESIÓN DE LORENTZ-

Al contrario que en los campos eléctricos, una partícula cargada que se encuentre en reposo en el interior de un campo magnético no sufre la acción de ninguna fuerza. Otra caso bien distinto se produce cuando la partícula se encuentre en movimiento, ya que por el contrario, en este caso, la partícula si que experimentará la acción de una fuerza magnética que recibe el nombre de fuerza de Lorentz.

Carga en un campo magnético. Cuando se introduce una carga en reposo dentro de un campo magnético este no ejercerá ninguna acción sobre ella dejándola tal y como se encontraba, es decir, en reposo (figura 1). Si por el contrario (figura 2), la carga que se introduce se encuentra en movimiento experimentará una fuerza capaz de provocar cambios en la dirección de su velocidad y por tanto en su trayectoria.

Por tanto, los campos magnéticos son generados por cargas en movimiento y sólo ejercen una acción sobre cargas eléctricas que se encuentran en movimiento

La ley de Lorentz establece que una partícula cargada q que circula a una velocidad v→ por un punto en el que existe una intensidad de campo magnético B→, sufrirá la acción de una fuerza F→ denominada fuerza de Lorentz cuyo valor es proporcional al valor de q, B→ y v→  se obtiene por medio de la siguiente expresión:

F→=q⋅v→×B→

De la ecuación anterior podemos extraer las siguientes conclusiones:

  • Su módulo es F=|q|⋅v⋅B⋅sin α, donde α es el angulo formado entre v→ y B→.
  • Su dirección es perpendicular al plano que forman v→ y B→ (debido al producto vectorial entre ambos vectores).
  • Su sentido será el de v→×B→ si q es positivo y el contrario si es negativo.

De una forma gráfica es posible determinar la dirección y sentido de la fuerza de Lorentz aplicando la regla de la mano derecha. Para ello sitúa tu mano derecha de tal forma que tu dedo índice coincida con la dirección y sentido del vector velocidad, el medio (o corazón) coincida con la dirección y sentido del campo magnético. Si la carga es positiva, tu dedo pulgar estará indicando la dirección y sentido de dicha fuerza. Si es negativa estará indicando su dirección aunque el sentido será el contrario del que marca tu pulgar.

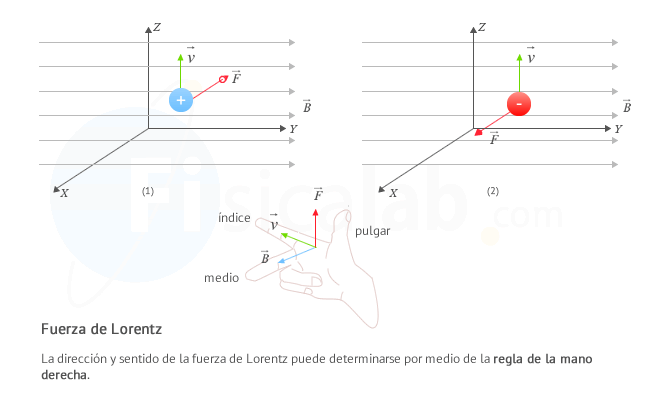
La fuerza de Lorentz se puede obtener gráficamente aplicando la regla de la mano derecha.

En resumen, según la expresión de la ley de Lorentz la fuerza de Lorentz será:

  • Nula
    • ​Si la partícula no posee carga. q = 0 -> F = 0.
    • Si la partícula está en reposo. v = 0 -> F = 0. 
    • Si la velocidad de la partícula es paralela al campo. F = |q|·v·B·sen 0 -> F = 0
  • Máxima. Si v y B son perpendiculares ( α = 90º ) entonces F = |q|·v·B·sin 90 = |q|·v·B.

Comentarios

Publicar un comentario

Entradas populares