-FUERZA SOBRE UN CONDUCTOR POR EL QUE CIRCULA UNA CORRIENTE-

Un conductor puede ser un cable o alambre por el cual circula una corriente eléctrica. Una corriente eléctrica es un conjunto de cargas eléctricas en movimiento. Ya que un campo magnético ejerce una fuerza lateral sobre una carga en movimiento, es de esperarse que la resultante de las fuerzas sobre cada carga resulte en una fuerza lateral sobre un alambre por el que circula una corriente eléctrica.

Conductor rectilíneo

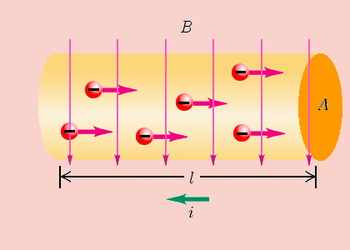
En la figura se muestra un tramo de alambre de longitud ${\displaystyle \scriptstyle l}$ que lleva una corriente ${\displaystyle \scriptstyle i}$ y que está colocado en un campo magnético ${\displaystyle \scriptstyle \mathbf {B} }$. Para simplificar se ha orientado el vector densidad de corriente ${\displaystyle \scriptstyle \mathbf {j} }$ de tal manera que sea perpendicular a ${\displaystyle \scriptstyle \mathbf {B} }$.

La corriente ${\displaystyle \scriptstyle i}$ en un conductor rectilíneo es transportada por electrones libres, siendo ${\displaystyle \scriptstyle n}$ el número de estos electrones por unidad de volumen del alambre. La magnitud de la fuerza media que obra en uno de estos electrones está dada por;

${\displaystyle F^{\prime }=q_{0}vB\sin \theta =ev_{d}B}$

por ser ${\displaystyle \,\!\theta =90^{\circ }}$ y siendo ${\displaystyle \,\!v_{d}}$ la velocidad de arrastre: ${\displaystyle v_{d}={\frac {j}{ne}}}$. Por lo tanto,

${\displaystyle F^{\prime }=e\left({\frac {j}{ne}}\right)B={\frac {jB}{n}}}$

La longitud ${\displaystyle \scriptstyle l}$ del conductor contiene ${\displaystyle \scriptstyle nAl}$ electrones libres, siendo ${\displaystyle \scriptstyle Al}$ el volumen de la sección de conductor de sección transversal ${\displaystyle \scriptstyle A}$ que se está considerando. La fuerza total sobre los electrones libres en el conductor y, por consiguiente, en el conductor mismo, es:

${\displaystyle F=\left(nAl\right)F^{\prime }=nAl{\frac {jB}{n}}}$

Ya que ${\displaystyle \scriptstyle jA}$ es la corriente ${\displaystyle \scriptstyle i}$ en el conductor, se tiene:

${\displaystyle \,\!F=ilB}$

Las cargas negativas que se mueven hacia la derecha en el conductor equivalen a cargas positivas moviéndose hacia la izquierda, esto es, en la dirección de la flecha verde. Para una de estas cargas positivas, la velocidad ${\displaystyle \,\!v}$ apuntaría hacia la izquierda y la fuerza sobre el conductor ${\displaystyle \,\!F=q_{0}v\times B}$ apunta hacia arriba saliendo del plano de la figura. Esta misma conclusión se deduce si se consideran los portadores de carga negativos reales para los cuales ${\displaystyle \,\!v}$ apunta hacia la derecha, pero ${\displaystyle \,\!q_{0}}$ tiene signo negativo. Así pues, midiendo la fuerza magnética lateral que obra sobre un conductor con corriente y colocado en un campo magnético, no es posible saber si los portadores de corriente son cargas negativas moviéndose en una dirección o cargas positivas que se mueven en dirección opuesta.

La ecuación anterior es válida solamente si el conductor es perpendicular a ${\displaystyle \,\!B}$. Es posible expresar el caso más general en forma vectorial así:

${\displaystyle \mathbf {F} =i\scriptstyle \mathbf {l} \times \scriptstyle \mathbf {B} }$

siendo ${\displaystyle \scriptstyle l}$ un vector (recorrido) que apunta a lo largo del conductor en la dirección de la corriente. Esta ecuación es equivalente a la relación ${\displaystyle \scriptstyle \mathbf {F} =q_{0}\mathbf {v} \times \mathbf {B} }$ y cualquiera de las dos puede tomarse como ecuación de definición de ${\displaystyle \scriptstyle \mathbf {B} }$

Obsérvese que ${\displaystyle {\vec {l}}}$ (no representado en la figura) apunta hacia la izquierda y que la fuerza magnética ${\displaystyle ({\vec {F}}=i{\vec {l}}\times {\vec {B}})}$ apunta hacia arriba saliendo del plano de la figura.

Esto concuerda con la conclusión a que se llegó al analizar las fuerzas que obran en los portadores de carga individuales.

Conductor no rectilíneo

Si se considera solamente un elemento diferencial de un conductor de longitud ${\displaystyle \scriptstyle d\mathbf {l} }$, la fuerza ${\displaystyle \scriptstyle d\mathbf {F} }$ puede encontrarse mediante la expresión

${\displaystyle \mathbf {F} =\int _{L}i(d\mathbf {l} \times \mathbf {B} )}$

Considérese, por ejemplo, un alambre de la forma mostrada en la figura, que lleva una corriente i y se encuentra en el seno de un campo magnético uniforme de inducción magnética ${\displaystyle \,\!B}$ saliendo del plano de la figura tal como lo muestran los puntos. La magnitud de la fuerza sobre cada tramo recto está dada por:

${\displaystyle \,\!F_{1}=F_{3}=ilB}$

y apunta hacia abajo tal como lo muestran los vectores coloreados de verde. Un segmento de alambre de longitud ${\displaystyle \,\!d{\vec {l}}}$ en el arco experimenta una fuerza ${\displaystyle d{\vec {F}}}$ cuya magnitud es:

${\displaystyle \,\!dF=iBdl=iB(Rd\theta )}$

y cuya dirección es radial hacia O, que es el centro del arco. Solamente la componente hacia abajo de esa fuerza es efectiva, porque la componente horizontal es anulada por una componente directamente opuesta proveniente del correspondiente segmento de arco a la derecha de O. En consecuencia, la fuerza total sobre el semicírculo de alambre alrededor de O apunta hacia abajo y es:

${\displaystyle F_{2}=\int _{0}^{\pi }dF\sin \theta =\int _{0}^{\pi }(iBRd\theta )\sin \theta =iBR\int _{0}^{\pi }\sin \theta d\theta =2iBR}$

Entonces, la fuerza total será:

${\displaystyle \,\!F=F_{1}+F_{2}+F_{3}=2ilB+2iBR=2iB(l+R)}$

Es interesante notar que esta fuerza es la misma que obraría sobre un alambre recto de longitud ${\displaystyle \,\!2l+2R}$

https://es.wikipedia.org/wiki/Fuerza_magn%C3%A9tica#:~:text=Una%20corriente%20el%C3%A9ctrica%20es%20un,que%20circula%20una%20corriente%20el%C3%A9ctrica.